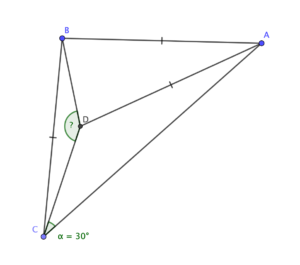
A puzzle from @Barney_MT:
Find angle BDC
This turns out to be a bit more demanding than I expected. There are spoilers below the line, showing a solution that took rather more time and space than the final polished version does. Spoilers below the line!
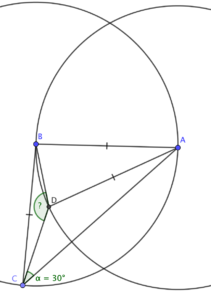
Adding in circles
When I’ve got isosceles triangles knocking about, I like to add in some circles. Circle theorems, as much as I think they’re a bit of a gimmick at GCSE, are quite useful in geometry puzzles.
Now, how do these circles help?
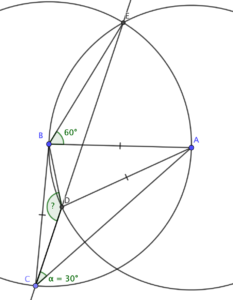
How about that top intersection?
The way the circles are set up, there’s an equilateral triangle formed by points A, B and the upper intersection of the circles - let’s call that point E.
Here’s the clever bit: C lies on the circle centred at B. Since chord AE subtends 60 degrees at B, it must subtend 30 degrees at C, meaning that E lies on the line CD!
That makes it easy.
Easy?!
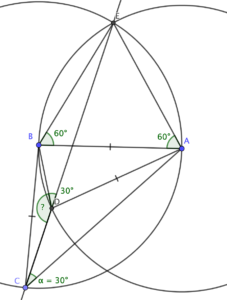
Now consider line segment BE, which is a chord of the circle centred at A. It subtends 60 degrees there, so it subtends 30 degrees at D, on the circle’s circumference.
And since CDE is a straight line, angle BDC must be 150 degrees.
I’d be curious to learn whether there’s a slicker way of doing that, perhaps one that doesn’t involve circle theorems! Drop me a comment if you can see one.